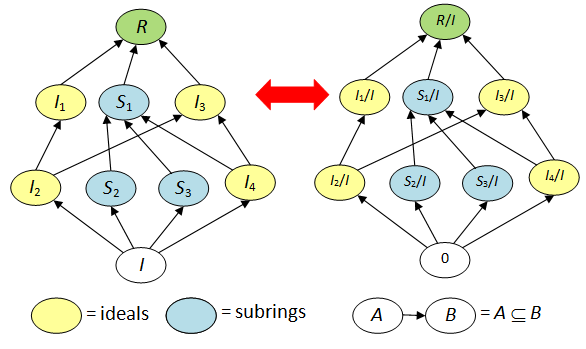
SOLVED: Give an example of a ring R in which every proper ideal is finitely generated but R is not Noetherian. If ab = ba for a, b ∈ R, prove that
rings | Math Counterexamples
Abstract Algebra | More examples involving rings: ideals and isomorphisms. - YouTube
6.6.4 Subring, Ideal and Quotient ring - ppt download
Amazon.com: iDeal Of Sweden Magnetic Ring Mount (Attachable Selfie & View Stand) (Silver) : Cell Phones & Accessories
27 Principal Ideal Domains and Euclidean Rings: 1 1 K K I I | PDF | Ring (Mathematics) | Abstract Algebra
MathType on Twitter: "Prime numbers are fascinating, aren't they? What about prime ideals!? This concept from ring theory generalizes the concept of prime numbers, and is key in algebraic #geometry and #NumberTheory. #
SOLVED: 2 (a) Show that every ideal in ring Z is principal. More specifi- cally; prove the following: if A is an ideal in Z; then A = (n) = nZ; where
Solved Exercise 27. Find all ideals of the following rings: | Chegg.com
abstract algebra - Visualizing quotient polynomial rings are fields for maximal ideals which are generated by irreducible monic - Mathematics Stack Exchange
![PDF] Formalization of Ring Theory in PVS Isomorphism Theorems, Principal, Prime and Maximal Ideals, Chinese Remainder Theorem | Semantic Scholar](https://d3i71xaburhd42.cloudfront.net/ad9be6262045ba725d366791d0badfcbd6010d9a/7-Figure2-1.png "PDF] Formalization of Ring Theory in PVS Isomorphism Theorems, Principal, Prime and Maximal Ideals, Chinese Remainder Theorem | Semantic Scholar")
PDF] Formalization of Ring Theory in PVS Isomorphism Theorems, Principal, Prime and Maximal Ideals, Chinese Remainder Theorem | Semantic Scholar
commutative algebra - Ideal of Definition - Mathematics Stack Exchange
Ally Learn - Quiz on Ring Theory PRIME Ideal of a Ring - A simple and useful concept in Ring Theory Learn the concepts of Higher Mathematics from about 900 video lectures
Ideals and Subrings
![SOLVED: Corollary 3.26: If (R+) is a principal ideal ring and is an ideal of R taken R, then [principal ideal Tng]. Proof. Exercise: Exercise 41: Let R+ be a ring with](https://cdn.numerade.com/ask_images/4f7377eb7f8540ffaee42e382328d693.jpg "SOLVED: Corollary 3.26: If (R+) is a principal ideal ring and is an ideal of R taken R, then [principal ideal Tng]. Proof. Exercise: Exercise 41: Let R+ be a ring with")
SOLVED: Corollary 3.26: If (R+) is a principal ideal ring and is an ideal of R taken R, then [principal ideal Tng]. Proof. Exercise: Exercise 41: Let R+ be a ring with
SOLUTION: Ring Theory notes (Ring ideals and it s types ) - Studypool
Definition: R is a ''principal ideal ring'' if R is | Chegg.com
abstract algebra - Why proper ideal doesn't contain $1$? - Mathematics Stack Exchange
group theory - Left ideal in a ring $R$ is a subgroup - Mathematics Stack Exchange
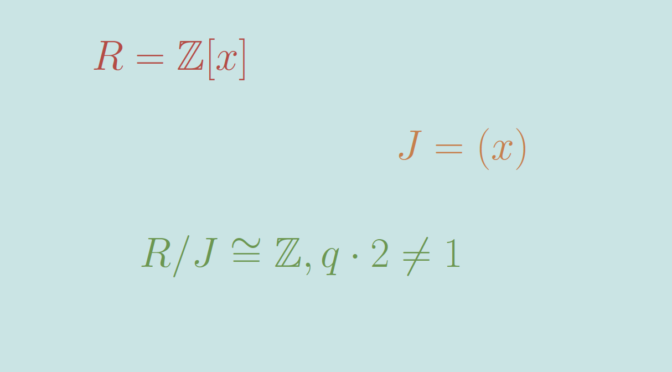
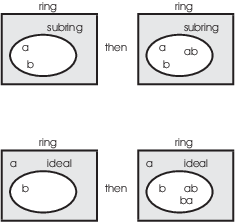
![PDF] Signature Standard Bases over Principal Ideal Rings | Semantic Scholar](https://d3i71xaburhd42.cloudfront.net/651ba51c455156974f6cee98ca07a2ec9b01b236/146-Table3.2-1.png "PDF] Signature Standard Bases over Principal Ideal Rings | Semantic Scholar")
PDF] Signature Standard Bases over Principal Ideal Rings | Semantic Scholar
Introduction to Ring Theory (5) | Mathematics and Such
Ideal - Left Ideal And Right Ideal - Definition - Ring Theory - Algebra - YouTube
Q)Chapter-14(ring theory) - Chapter - 14 (Ideals and Factor Rings) Dr. Sunil Kumar Yadav and Ms. - Studocu
